Serendip is an independent site partnering with faculty at multiple colleges and universities around the world. Happy exploring!
Deterministic and Non-deterministic Emergence: Deterministic Emergence
In A New Kind of Science, Stephen Wolfram outlines an instance of the more general emergence approach using the basic insight that one may indeed get a quite substantial array of patterns out of simple things interacting in simple ways, which we call "deterministic emergence". While this approach is not at all unique to Wolfram, he systematically explored it in a way that leads both to some important additional understandings and to some interesting new issues. We will use both the potentials and limitations of "deterministic emergence" to clarify, further characterize, and explore an alternative approach to making sense of the world, which we call "non-deterministic emergence", that we believe is also worth taking seriously.
|
Inquiry approach 2
Deterministic emergence Goal: to characterize the starting conditions and rules (initial pattern) from which everything else follows over time Perception of time/evolution: essential as the parameter underlying emergence Status of disorganization: along with later patterns, the product of the initial pattern |
Cellular automata are a widely explored instance of "simple things interacting in simple ways that can yield surprisingly complex outcomes," with the additional feature that both the things and their interactions are "deterministic," i.e. any given set of things, interactions, and starting conditions will always yield the same result. Among the simplest of cellular automata is a linear array of elements each of which can exist in one of only two states, together with a rule set that transforms any given linear array into a new one based on the state of each element and its two neighbors. Since one element can be in either of two states, there are eight possible states for an element and its two neighbors. A rule set specifies what the subsequent state of the element will be for each of the eight possible states of that element and its neighbors. There are two possible outcomes for each of the eight possible states, and therefore 2x2x2x2x2x2x2x2 = 256 possible rule sets. Wolfram systematically explored the pattern generating capabilities of each of these 256 rule sets (as you can using the model here) and a variety of others. From these came some important conclusions about deterministic systems:
- Simple interactions of simple things do indeed yield patterns that one doesn't expect (assuming you have never seen it happen before).
- Simple interactions of simple things yield results that cannot be determined in advance, i.e. for some starting conditions and rule sets there is no way to determine what will result except by trying it out.
- Simple interactions of simple things can produce both patterns and what appears to be disorganization.
- Making things and their interactions more complex doesn't increase the complexity of the resulting patterns.
With this understanding in mind, let's look a bit more at each of the conclusions.
Conclusions 1 and 2. " ... yield patterns that one doesn't expect..." and "... yield results that could not be determined in advance"
The "surprise" here is of two sorts. The first has to do with what an observer expects and doesn't expect of simple interactions of simple things. If one thinks that pattern depends on a designer or architect, one is surprised to see it appear in the absence of either. Once one gets used to the emergence perspective, there is less surprise on this count.
The other source of surprise is that there exist processes for which every step is fully defined ("algorithmic processes") but where the outcome can't be known except by carrying out each step. If one has, for one reason or another, come to believe that there is an "equation" for all well-defined processes, one that will allow one to determine the state of the system at all future times by plugging in a value of time, this is not only a surprising but an important new understanding. If one has a greater familiarity with the work of Turing and others, the point is not less important but is less surprising.
Wolfram makes more of this point, saying he suspects it "is the ultimate origin of the apparent freedom of human will... even though all the components of our brains presumably follow definite laws, I strongly suspect that their overall behavior corresponds to an irreducible computation whose outcome can never in effect be found by reasonable laws." We'll return to this issue below.
3. "... produce both patterns and what appears to be disorganization..."
|
(click to enlarge)
Figure 1
|
At this point, we need to be more explicit about what one means by "pattern" as well as by "disorganization." Most people looking briefly at Figure 1 would agree that it is "disorganized" in the sense that it exhibits no pattern. But others may see patterns in it from the outset, and others may begin to see patterns if they look at it long enough. The human brain has evolved to find patterns, and so one's judgement that something is disorganized because it has no pattern is not a very reliable one.
Figure 1 is, however, "disorganized" or "unpatterned" in a less subjective sense. Each element that makes up the figure can be in either of two states (black or white), each has a 50% probability of being on or off, and whether one is on or off is completely independent of the state of any other element. To put it differently, there is no correlation whatsoever between the state of one element in the image and the state of any other element. Knowing the state of one element does not give one any information useful in predicting the state of any other. In this sense, Figure 1 is fully disorganized, lacking any pattern; the distribution of black and white is random. Figure 2 is at the other end of a spectrum. Once one knows the distribution of blacks and whites over a small part of the figure, one knows it over the entire figure. There's a pattern. The same is true of Figure 3. Figure 4 and 5, on the other hand, seems to have local areas of pattern as well as local areas lacking pattern.
The surprise here is in important ways the converse of the surprise associated with point 1. Simple interactions of simple things can yield patterns that one doesn't expect" AND yield disorganization, absence of pattern. Not one or the other but both. It is not only order that can result from simple interactions of simple things but lack of order, statistical randomness, as well. Perhaps then, as Wolfram suggests, simple deterministic interactions of simple deterministic things can produce everything we experience around us, everything we could experience? Perhaps deterministic emergence actually could be a sufficient basis for making sense of the world?
At this point we need to flag the notion of "statistical randomness". What one can conclude from observations of cellular automata (and in other mathematical explorations), is that deterministic systems are capable of producing results that look to be indistinguishable from the results of non-deterministic systems (ones in which the current state allows several different possible next states). Another way to say the same thing is that any known output of a system, no matter how much pattern it does or does not have, can be generated by a deterministic system. That is not quite the same thing as saying that there is in principle no distinction whatsoever between deterministic and non-deterministic systems (see On Beyond "On Beyond Newton" and Variability in Brain Function and Behavior). We'll discuss this further below; it's a critical issue in deciding whether indeed "deterministic" emergence is an adequate basis for making sense of the world.
4. "Making things and their interactions more complex doesn't increase the complexity of the resulting patterns"
Here too we need to be more explicit about terms, in this case what is meant by "complex". Wolfram's point is that something as simple as a cellular automaton is capable of doing exactly the same set of computations as any serial computer, no matter how sophisticated. And that certainly may surprise people unless, again, they are familiar with the work of Turing and others following him. A "Turing machine" is also a deterministic interaction of simple elements interacting deterministically in simple ways and, like a cellular automaton, it is also capable of doing exactly the same set of computations as any contemporary (or conceivable) serial computer. The point is an important one if one is thinking about computers, or about information processing more generally. And it is an even more important one if one thinks that the brain is subject to the same limitations as a cellular automaton or a Turing machine. But do we need to presume it is? Or can there be things in the world, our world, beyond those that a cellular automaton or Turing machine is capable of creating? That's the question to which we turn in the next section.

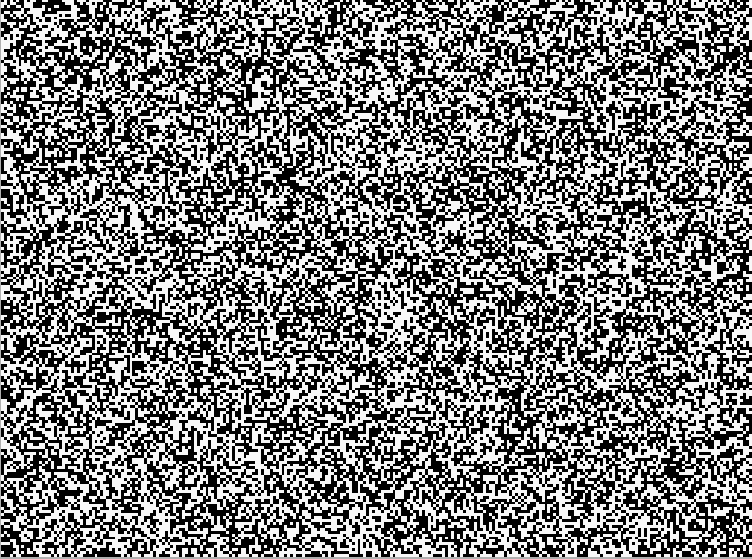
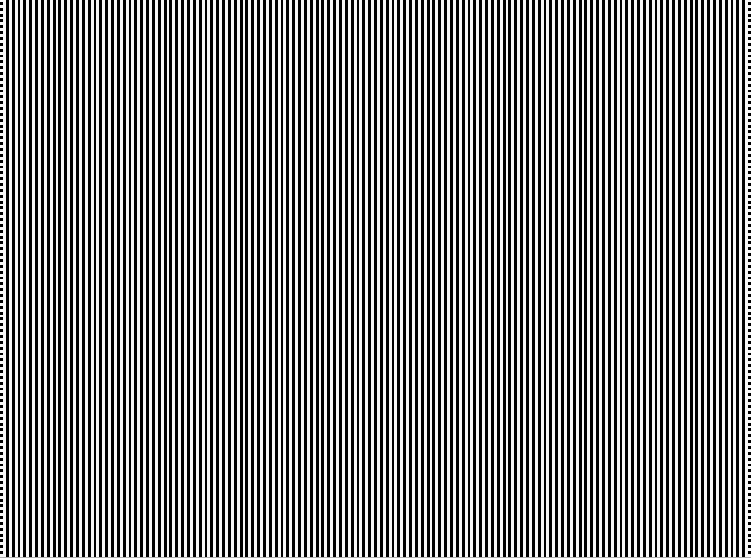





Comments
Post new comment