Home Page

Compare Brains

Compare Brain and Body Sizes

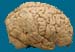
Compare Brain Structures- Slices and Slides

The Neuron- Up Close and Personal

The Question of Intelligence
  1. absolute size
  2. brain/body size
  3. cortical folding
  4. neocortex
  5. gray matter/nerve cells
  6. specific brain structures

Links

Glossary

Bibliography

Thinking about Brain Size...

A first most obvious manner of comparison would be the ratio of body weight to brain weight. Using Cuvier's fraction E/S (where E=brain weight and S= body weight), we find the following ratios:

Cat: 1/100; Dog: 1/120-1/300; Lion: 1/550; Horse: 1/600; Hippopotamus: 1/2789; Human: 1/40; Mouse: 1/40; Elephant: 1/560; small birds: 1/12; Frog: 1/172; Shark: 1/2496.

Notice that the human and mouse ratios are roughly identical and the horse and elephant ratios are also roughly identical. Note also that these ratios are according to relative brain weights from adult individuals.

However, a complexity in this method is that brain weight in vertebrates does not in general appear to increase linearly with body weight, so that heavy vertebrates have proportionally smaller brains than light vertebrates, and many small mammals have, in terms of these simple ratios, relatively larger brains than that of humans. . .


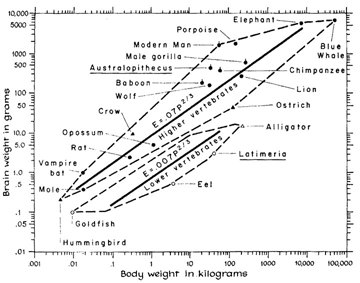
(image thanks to www.neurophys.wisc.edu)

The figure above tells us about the brain/body relations of several familiar animals. Essentially, we see that brain size increases with body size in a specific exponential rate.

This may lead us to question-- if the increase in brain weight that accompanies increases in body weight does not necessarily increase intelligence, what then is the function of the 'extra' brain matter?

In order to remedy inconsistencies in the simple ratio method, let us try "allometry" (link- glossary: the science of relating quantitatively the size of one part of the body to another). The following equation was developed in the late 19th century by Snell: E=CS^r, where E is the weight of the brain, S the body weight, C is a constant "cephalization factor", and r an epirically determined exponential constant. Kuhlenbeck suggests this value to be around 0.56 for mammals. Macphail asserts that this exponent would be approximately 0.66 for most mammals.

Once an acceptable value of r is determined, then we see that brain weight is determined by two other factors, S, the body weight and C, the cephalization factor. This equation, then, gives us a way of establishing the relative capacity of brains of different species with different body weights. When we enter values for the weights of brains and bodies of two species, then a value of C can be determined for each species. We can then find the encephalization quotient (EQ) which is the ratio of C over the average mammalian value. For example, if a certain species has an EQ of 2.0, this means that the species has a value of C twice as high as that expected in a mammal of comparable weight with average encephalization. Or if a species has an EQ of 0.5, then this species has a level of encephalization half that of an "average" mammal" (link- once again,what is normal?). Let us look at the following table of encephalization quotients (using Macphail's 0.66 as the constant r value):

Species EQ Species EQ
Man 7.44 Cat 1.00
Dolphin 5.31 Horse 0.86
Chimpanzee 2.49 Sheep 0.81
Rhesus Monkey 2.09 Mouse 0.50
Elephant 1.87 Rat 0.40
Whale 1.76 Rabbit 0.40
Dog 1.17 (Macphail, 243)

Does this information agree with your intuitions regarding relative intelligence of mammals? We see that man is at the top, with dolphins a close second, and on down. Dolphins have a high reputation for intelligence, but do we also assume that dogs are more intelligent than cats? How do we determine if a mouse is more intelligent than a rat? This data seems to indicate that higher primates are generally more "encephalized" than lower primates relative to mammals as a whole and that smaller mammals and rodents are below average.

None of this data necessarily has a definitive link with intelligence. Only behavioral data could show the significance of levels of encephalization of a species. Let's look at other methods for comparing species' brains before we make any final conclusions as to the relevance of this information.

What about cortical folding and intelligence?

I want to go back to brain and body size

Huh? Can we start over?