The Three Doors of Serendip:
"Rational Understanding"



The Three Doors of Serendip:
|    |
| Door image from http://www.woodstone.com/photoalbum7.html |
Welcome through the third of the Three Doors of Serendip. If you haven't been through the first two, you might want to do so. You should at least check out the first one so you know the rules are of the Three Door game we're talking about here ... and using as a way to better understand understanding.
Behind each of the first two doors are things you can do things with. Here, we just want to consider a question. Below are two different explanations of what the best strategy is for playing the Three Door game ... leading to two quite different conclusions. All you have to do is to decide which one is right.
| EXPLANATION 1 | EXPLANATION 2 |
| After one sees the prize is not behind the first door opened, one knows there are only two places the prize can be ... and nothing more. Therefore, the prize has the same chance of being behind either of two remaining doors. Pick either one; it doesn't matter. | There is one chance in three that the door you first picked is the correct one. This can't change just because you're shown there isn't a prize behind some other door. Since the prize has to be behind either the door you picked or the other closed door, and there is one chance in three that its the one you picked, there must be two chances in three its behind the other door. Switch, and you'll be right twice as often |
Let's briefly review the rules, to be sure we're on the same wavelength and to introduce you to the details of the game implementation available here for your experiments.  When you click here, the implementation will come up in a separate window (don't do this if you already have the implementation on your screen), looking something like the screen shot to the left below (be patient, the applet will take a little time to load, and you may have to resize the window by dragging the bottom corner). There are three doors (numbered at the top), with a prize (in this case, access to the wonderful land of Serendip; see figure to right) hidden randomly behind one of them.
When you click here, the implementation will come up in a separate window (don't do this if you already have the implementation on your screen), looking something like the screen shot to the left below (be patient, the applet will take a little time to load, and you may have to resize the window by dragging the bottom corner). There are three doors (numbered at the top), with a prize (in this case, access to the wonderful land of Serendip; see figure to right) hidden randomly behind one of them.  You pick one of the three doors, after which Serendip will show you that one of the two remaining doors is NOT where the prize is (instructions for each step of the game will appear in the yellow bar across the middle of the display). At this key point in the game, you will be asked whether you want to stay with your original choice or switch to the remaining unopened door. After you make your choice, Serendip will show you whether you've won or not, recording both that and your choice, and invite you to continue playing, as many times as you like. A cumulative total of your choices and the results will be kept by Serendip, and displayed when you click the yellow bottom to the right at the bottom of the implementation. Click the left bottom button to start, and again whenever you want to reset the implementation to start a new collection of observations.
You pick one of the three doors, after which Serendip will show you that one of the two remaining doors is NOT where the prize is (instructions for each step of the game will appear in the yellow bar across the middle of the display). At this key point in the game, you will be asked whether you want to stay with your original choice or switch to the remaining unopened door. After you make your choice, Serendip will show you whether you've won or not, recording both that and your choice, and invite you to continue playing, as many times as you like. A cumulative total of your choices and the results will be kept by Serendip, and displayed when you click the yellow bottom to the right at the bottom of the implementation. Click the left bottom button to start, and again whenever you want to reset the implementation to start a new collection of observations.
Playing Around With Experiments
Got some intuitons/ideas that you want to test? If so, go to it. Remember though that you need to have not one but two "strategies" in mind for a good experiment, one strategy that you think is better and one that you think is less good. Play the first strategy for a number of games and then find out from Serendip how well you did by clicking the yellow botton on the implementation. You'll see and display like that to the left (but reflecting the number of games you played and the results).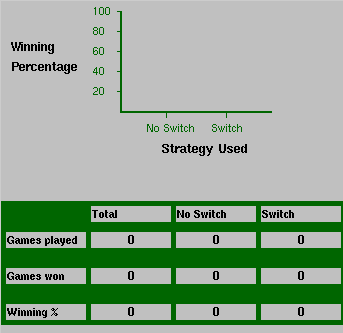 All you have to worry about here is the "Total" column at the bottom, which will show you the number of games you played with that strategy, the number of times you won, and the percentage of games won using that strategy. Reset and then play your second strategy for a number of games, and then see whether you did better or worse the second time. Remember too, though, that there's some randomness in the game, so "a number of times" should be pretty big number (ten or twenty at least), and you shouldn't take small differences in the outcomes too seriously (do the comparison several times to see whether any differences you observe are reliable).
All you have to worry about here is the "Total" column at the bottom, which will show you the number of games you played with that strategy, the number of times you won, and the percentage of games won using that strategy. Reset and then play your second strategy for a number of games, and then see whether you did better or worse the second time. Remember too, though, that there's some randomness in the game, so "a number of times" should be pretty big number (ten or twenty at least), and you shouldn't take small differences in the outcomes too seriously (do the comparison several times to see whether any differences you observe are reliable).
Not sure what to test? Then here's a suggestion. Since the prize is randomly placed behind any one of the three doors at the beginning of each game, your first choice in each game probably doesn't make any difference, and it probably also doesn't make any difference what you did or what happened during the previous game. If this is true, then all that matters is whether you stay or switch with your second choice on each game. Hence the problem boils down to three possibilities: staying is better, switching is better, or it doesn't matter whether you stay or switch. You can explore all three possibilities by comparing two strategies: always stay with your second choice and always switch with your second choice. If one reliably does better, you've established that that one is the better strategy; if neither reliably does better, then it doesn't matter whether you switch or stay. Either, as well as choosing randomly each time, is an equally good strategy.
You can test whether stay or switch is the best strategy by playing a series of games using one strategy, finding out the percentage of times you win, then doing the same with the other strategy, and comparing the two percentages (see above). Serendip also provides a "short cut" for this particular comparison of strategies. If you play series of games, sometimes using the stay strategy and sometimes using the switch strategy Serendip stores and displays the results separately for the two strategies (see the figure above). So you can intermingle stay and switch strategies and still see whether either has a higher winning percentage.
It turns out that ....(spoiler) . Is that what you expected? Are you surprised? No, Serendip is not "rigged". The prize is actually put behind a randomly selected door at the outset of each game, and stays there through that game. Serendip knows which door this is, and hence knows which door it can safely open (choosing randomly between two possibilities in some cases). If you're still skeptical about Serendip cheating, you can play the game with some home-made equipment and a friend; the answer will come out the same.
 |
 |
 |
|
"Hands on" understanding intuitive, unconscious | "Experimental" understanding conscious, observational | "Rational" understanding conscious, analytical, logical |