Remote Ready Biology Learning Activities has 50 remote-ready activities, which work for either your classroom or remote teaching.
Serendip is an independent site partnering with faculty at multiple colleges and universities around the world. Happy exploring!
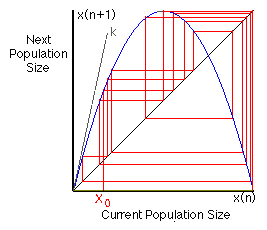 So ... simple rules can lead to stability (homoeostasis) if the value of one parameter is small or to oscillation (autonomy) if that parameter is a little bigger. So what happens if that parameter is a little bigger still? Good question. With an important answer,which a picture can hint at (as the one at the right does) but can't do justice to. For steeper curves (larger k values), things get pretty crazy and you have to actually see it happening. So, we're best off if we let Serendip do the plotting from the beginning (remember to click even if you already have the extra window up from previous pages). If you haven't worked through some of the earlier pages, you'll probably want to do that, or you won't understand what's being plotted.
So ... simple rules can lead to stability (homoeostasis) if the value of one parameter is small or to oscillation (autonomy) if that parameter is a little bigger. So what happens if that parameter is a little bigger still? Good question. With an important answer,which a picture can hint at (as the one at the right does) but can't do justice to. For steeper curves (larger k values), things get pretty crazy and you have to actually see it happening. So, we're best off if we let Serendip do the plotting from the beginning (remember to click even if you already have the extra window up from previous pages). If you haven't worked through some of the earlier pages, you'll probably want to do that, or you won't understand what's being plotted.
This time, we're looking at an even steeper inverted curve relating current to next population size (k=3.9). Click below the x-axis to select a starting value and then start interating. No staircase to a stable point, huh? Well, how about a box that gets smaller or bigger and then stays the same, an oscillation? Sometimes it looks like that's what's happening, but then, all of a sudden, the values start changing again. You've entered the realm of chaotic behavior. The underlying rules are simple, but the outcome is neither constant nor describable in terms of any regular variation. There is no reliable regularity in the variation. In fact, if you didn't know the simple rule underlying the system, there is no way at all that you could predict for sure the next population size regardless of how carefully you study the variations in the previous history of the population.
You'll want to check this yourself by trying different x values (and by looking at later stages of sets of iterations, using the "Interations" and "Skip first" controls). Can it really be true that simple rules lead to highly unpredictable behavior? Yes, indeed, its really true. As you'll find out for yourself. Values may, at any given time, get close to values they had before, but they never quite match them perfectly (if they did, then you would be able to predict what would happen next, and next, and next ...).
Why is this so? What makes these systems so different from those that Newton had in mind? and that many people think of as the norm? Recall that, in the case of populations, we wanted a rule such that smaller populations could lead to larger ones but larger populations could lead to smaller ones. What that means is that the rule is "non-linear": applying the rule to a population twice the size of a given population does not always lead to twice the result in the next population (as it would in a "linear" system"), but may result instead in a smaller size in the next population. And what that means, in general, is that what is going to happen next is not pretty much the same for similar starting values (as in "linear" rules), but rather highly dependent on the exact starting values: slightly different starting values can lead to enormously different outcomes.
This "non-linearity" is inherent in the inverted U-shaped curve ... and in lots of other rules. Because of it, such systems display what is called "a sensitive dependence on initial conditions" ... what happens next is critically dependent on the exact value at a given time. Small differences in the starting point do not necessarily mean small differences in the outcome; instead, the differences can be very large. And, with further iterations, even more different. This too you can get a feel for yourself, by letting Serendip plot some values for you, keeping k constant and seeing what happens with small change in x.
How come Newton didn't think about rules causing disorder, when he was thinking up ways to describe how apples fall, and planets move? And why do why all get taught that rules are what accounts for order, when they can equally create unpredictability? That probably has lots of answers. Newton, of course, was trying to account for some orderly things, not some disorderly ones (though it turns out that some planetary movements may actually be less ordered and more chaotic than Newton thought), so its not his fault. And, prior to the ready availability of computers, it simply wasn't possible to study iterative systems of the kind you're looking at here. With pencil and paper, it would take, for even one set of x and k values, enormous amounts of time to convince onself that the system never settles down, and there aren't any simple ("linear") equations one can solve to answer the question. Who was going to try and persuade oneself (to say nothing of anyone else) that never settling down was true for many such sets of values?
Its also true that many people like predictability better than unpredictability. Predictability makes things easier to deal with, in all sorts of obvious ways, and is a lot easier to establish, so these things too probably contributed to how long it took for people to accept that simple causes can have unpredictable effects. Appreciating the virtues of unpredictability is doable but a little harder. Regardless, substantial unpredictability does emerge in surprisingly simple well-ruled situations, and this, like autonomous behavior in such systems is worth keeping in mind. Its also very much worth thinking about where else the idea of unpredictability in rule-based systems might apply. Again, Newton's rule that systems at rest tend to stay at rest unless acted on by an outside force is not a good generalization. Lots of systems may change in unpredictable ways for reasons entirely inside the system. Does that fit your experiences of mood? Of the stock market? Of life in general? And systems may change from stable to oscillatory to "chaotic" with small changes in internal parameters. What might those parameters be? If one could identify them, then ...?
The bottom line?. With non-linear rules, one can get substantial unpredictability in behavior of rule-based systems. And that in turn, in addition to its general significance, has led to a whole new field of study: that of "non-linear dynamical systems", which we'll explore a bit in the next section. Such systems, it turns out, actually display a fair amount of order in their unpredictability, as we'll see. And that order from chaos is very interesting, from a lot of points of view.
At the same time, its worth noting again that lots of people don't like unpredictability. So, ironically, one of the reasons why people do like chaotic systems is that they are rule-based, and hence, in some sense, predictable. For those who actually do like unpredictability, an important reassurance is the fact that finding both a certain kind of unpredictability as well as order in rule-based chaotic systems doesn't make a more fundamental kind of unpredictability disappear. The unpredictibility of chaotic systems is quite different from non-rule based unpredictability, precisely because it does have one or another underlying rule. Coin flips, quantum phenomena, and the like represent "non-deterministic" unpredictability, an unpredictability with no underlying rule. While its hard to know which kind one is dealing with in any given case, the distinction is one with significant philosphical implications. In addition, not only chaotic systems but also systems which include a truly non-deterministic unpredictability can give rise to order. While deterministic unpredictability reveals new kinds of order, and helps account for a number of natural pheneomena, some examples of order are critically dependent on non-deterministic rather than chaotic unpredictability, and this is probably true of a variety of natural phenomena as well.
You know, Serendip and I have been plotting away, and I have the feeling that there's more order here than you're letting on, that there is a a way to say what's going to happen for different sets of x and k values. Can we look at that question?
I still think something doesn't add up. Take me back to the beginning, will you?
| Forum
| Complexity | Serendip Home |