Remote Ready Biology Learning Activities has 50 remote-ready activities, which work for either your classroom or remote teaching.
A digital ecosystem, fueled by serendipity.
Serendip is an independent site partnering with faculty at multiple colleges and universities around the world. Happy exploring!
Its always a good idea to start with something concrete and simple, and then see what one can do to generalize from it. So here's a concrete question: why is the population size of organisms (humans or otherwise) stable in some cases and variable in others? And here's a simple way to think about the problem. The population size at any given point in time is a major determinant of the population size at the next point in time (after all, it is the current population that produces the next population).
So let's imagine that there is some rule that relates population size in a next generation to that in the current generation. Such a rule might be as simple as "each organism in the current generation divides and gives rise to two organisms in the next generation". The problem with such a rule (and any of a large variety of variants of it) is that it would result in a population size that increases continuously and without limit. In fact, most populations seem to get larger if they are below some particular population size but to get smaller if they are above some particular population size (for any of a variety of reasons, such as overcrowding or limitations in available resources).
So we probably want a slightly less simple rule that expresses the property that population size in the next generation can be bigger for smaller population sizes in the current generation but also smaller for larger population sizes in the current generation. The figure shows an easy to imagine and visualize form of such a rule.
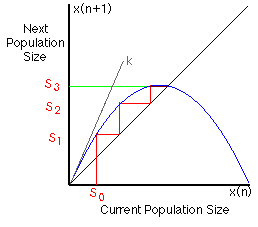The x-axis of the figure represents population size in the current generation and the y-axis the resulting population size in the next generation. The rule relating the two is the inverted blue curve, which gives for each current generation size (x axis) the population size in the next generation size (y axis). Notice that for smaller population sizes (to the left of the peak of the inverted curve), the population size of the next generation will be larger; for larger population sizes (to the right of the peak), the next generation will be smaller. There is also in the figure a line at forty-five degrees which helps to see what will happen to the population over time if one starts with a given population on the x axis.
Take a small initial population size (S0), for example. The red staircase shows how this initial population size will change over successive generations. In the generation after the initial one, the population size (S1) will be the value where the vertical red line for the initial population meets the population rule curve. This value is now the starting point for determining the population size in the subsequent generation. To do that, one can just extend the red horizontal line to the right until it meets the forty-five degree line (since x equals y anywhere on this line, this intersection simply transforms y (the just determined population size) into x (the current population size, from which we want to determine the next population size), and then run it straight up to the population rule curve. By repeating this process over and over again ("iterating"), one can determine the population size after any arbitrary number of generations.
In the case shown, the population quickly steps to a particular value (S3, as shown by the green line) at which, as we continue to apply the rule, it remains stable (since it falls on the x=y line, where current and next populations sizes are the same). That's interesting, and makes one wonder what would happen if one started with some other population size. Would it too reach a stable value? What value? And how about still other population sizes? The two examples shown below suggest that a stable value, in fact the same stable value, would be reached from any starting population size.
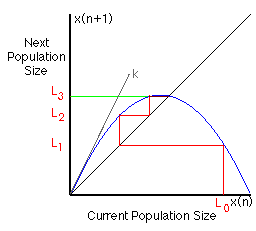
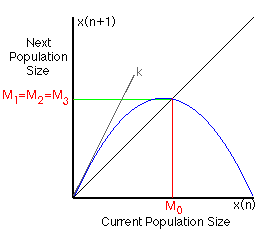
Now that's even more interesting. Is is really true that repeated application of this simple rule (which seems to itself say nothing whatsoever about any "final" population size) will always yield, from any starting point, a stable population size? That's the sort of thing you should always test yourself, rather than taking on faith. You could draw staircases from every starting point on a piece of paper, and verify that they all end up at the same place, but that would take a long time. To make it easier, we've arranged to have Serendip draw them for you; its a good example of how computers have made possible observations from which come important new perspectives. If you click on Serendip will draw them for you, a new window will appear on your desktop. Clicking below the x(n) axis will select an initial population size. Each click on the "iterate" button will give you the next population size, so with repeated clicks you can construct the whole staircase from any starting point you like. The graph above plots population size as a function of time, so you can see exactly how the population size changes as it approaches a stable value (sometimes increasing, other times decreasing along the way).
So ... we've got rules leading to order, as we might have expected. Be patient, we'll find that you don't have to change the rules very much to get some quite different things. And, in the meanwhile, its worth noting that the order we've found has some special characteristics and implications.
Imagine a population at the end of a staircase, and imagine further a famine which reduces population size, or a sudden inward migration which increases it. In terms of the figure, this simply means a sudden jump to a a new point on the x-axis. But any point on the x axis results in a new staircase back to the original point. Hence, one needs no additional rules to assure that disturbed populations will return to their original values; the ability to do so is inherent in the continual reapplication of the original rule.
The system defined by this simple rule displays one of the fundamental characteristics of living systems: it is homeostatic, responding to external perturbations with changes which return it to its original state. An ability to maintain the status quo can exist without an explicit defintion of the status quo, being instead inherent in the continuous application and reapplication of a simple set of rules.
Aright, I understand that simple rules can lead to dynamically maintained order. What's next?
Can I go back to the Introduction, please?
