| EXHIBIT UNDER DEVELOPMENT |
FROM RANDOM MOTION TO ORDER:
DIFFUSION AND SOME OF ITS IMPLICATIONS
"... we know all atoms to perform all the time a completely disorderly heat motion, which, so to speak, opposes itself to their orderly behavior and does not allow the events that happen between a small number of atoms to enrol themselves according to any recognizable laws. Only in the co-operation of an enormously large number of atoms do statistical laws begin to operate ... All the physical and chemical laws that are known to play an important part in the life of organisms are of this statistical kind; any other kind of lawfulness and orderliness that one might think of is being perpetually disturbed and made inoperative by the unceasing heat motion of the atoms" ....... Erwin Schrodinger, What Is Life?, 1944
Most people think of stability and order as the norm, the way things are ... and of movement and change as that which requires some explanation. Imagine a quiet lake in the forest, so still that the trees on the banks reflect downwards in it like a mirror. It ripples, distorting the image, if a fish jumps or you throw a pebble in or the wind blows. Undisturbed, it seems absolutely motionless, with a stability and order like glass.
In fact, as Schrodinger pointed out, it is not movement and change which requires explanation, but rather stability and order. What appears to us as a placid lake consists instead of an enormously large number of very very small water molecules all in continual motion, every one moving relatively independently of every other one.
That this is so not only of a forest lake, but of every other entity with which we have experience, including ourselves, represents a major advance in human understanding brought about by physicists in the late nineteenth and early twentieth centuries. It is an understanding with wide-ranging, and still to be fully explored, direct implications for physics, chemistry, and biology, and with at least metaphorical implications for thinking about a host of human phenomena as well. What phenomena of stability and order that we think we understand might better be understood in terms of underlying continous changes of constituent parts? What new insights might follow from reorienting one's thinking in that way?
To encourage your thinking about such questions, let's take a closer look at a simple example of an apparently stable and orderly system, and the underlying continuous motion of its constituent parts. How can continuous motion lead to an appearance of stability and order? What properties do such systems have that aren't present in systems that display order and stability for the "norm" reasons we expect (if such exist)? What can one do with systems displaying "dynamic order" that one couldn't do with other systems?
You can look into these and related questions in the following, using a Java applet to make your own observations. There are five pages following this one, as shown in the list below. Each is linked at the end to the next, or you
can go directly to any page, by clicking that page in the list. If you've worked through the exhibit, and just want to play more with the applet, you can click here. The entire text of the exhibit in one file is here.
Starting simple: from one moving part to many
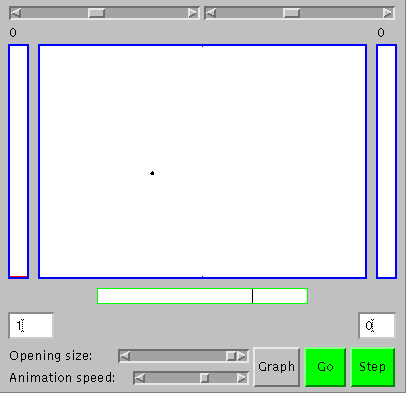 To appreciate stability and order based on underlying change, one first has to believe there are things changing, and then to see that certain kinds of stability and order emerge as the number of changing things increases ("statistical laws begin to operate", as Schrodinger put it). Let's start with a single moving particle in a large box, the green dot slightly to be left and below the center of the large rectangle (the large box) in the figure to the right, which shows the appearance of an applet we'll use for our explorations. You can get an active version of the applet elsewhere on your screen by clicking here. With it, you'll be able to see that the green dot is actually moving by clicking on the "Go" button. To see the movement more clearly, you can adjust the animation speed using the slider at the bottom of the applet, or click the "Step" button to get one frame at a time. The particle goes about its own business, following a straight line until it hits a wall of the box and then bouncing to follow a straight line until it hits another wall. That's not so surprising or interesting. What's more significant for us is that sometimes there is a particle in one half of the box and no particle in the other, and vice versa, as you can see from the numbers in the small boxes to the lower left and right of the applet. They both intermittently change from one to zero as the particle crosses the center of the box (the tall rectangles to the left and right in the applet also the number of particles on each side in the form of bar graphs, but that's not too impressive with only one particle; it'll be better when we get to working with more).
To appreciate stability and order based on underlying change, one first has to believe there are things changing, and then to see that certain kinds of stability and order emerge as the number of changing things increases ("statistical laws begin to operate", as Schrodinger put it). Let's start with a single moving particle in a large box, the green dot slightly to be left and below the center of the large rectangle (the large box) in the figure to the right, which shows the appearance of an applet we'll use for our explorations. You can get an active version of the applet elsewhere on your screen by clicking here. With it, you'll be able to see that the green dot is actually moving by clicking on the "Go" button. To see the movement more clearly, you can adjust the animation speed using the slider at the bottom of the applet, or click the "Step" button to get one frame at a time. The particle goes about its own business, following a straight line until it hits a wall of the box and then bouncing to follow a straight line until it hits another wall. That's not so surprising or interesting. What's more significant for us is that sometimes there is a particle in one half of the box and no particle in the other, and vice versa, as you can see from the numbers in the small boxes to the lower left and right of the applet. They both intermittently change from one to zero as the particle crosses the center of the box (the tall rectangles to the left and right in the applet also the number of particles on each side in the form of bar graphs, but that's not too impressive with only one particle; it'll be better when we get to working with more).
 Another way to say the same thing is that there is a change in the properties of the box (which side has particles) closely associated with a change in a property of the particle (its location). You can focus more on the changes in the state of the box by clicking on the "Graph" button on the active applet. This gives a display of the state of the box as a function of time, a snapshot of which is shown to the left. The middle grey line corresponds to both sides of the box being equally occupied by particles. More particles on one side is upwards from this line, and more particles on the other side downwards. With only one particle, the box repeatedly shifts from a state of all particles on one side (the upper broken red line) to a state of all particles on the other (the lower broken red line). There is, as we said above, a very close relation between a property of the particle and a property of the box.
Another way to say the same thing is that there is a change in the properties of the box (which side has particles) closely associated with a change in a property of the particle (its location). You can focus more on the changes in the state of the box by clicking on the "Graph" button on the active applet. This gives a display of the state of the box as a function of time, a snapshot of which is shown to the left. The middle grey line corresponds to both sides of the box being equally occupied by particles. More particles on one side is upwards from this line, and more particles on the other side downwards. With only one particle, the box repeatedly shifts from a state of all particles on one side (the upper broken red line) to a state of all particles on the other (the lower broken red line). There is, as we said above, a very close relation between a property of the particle and a property of the box.
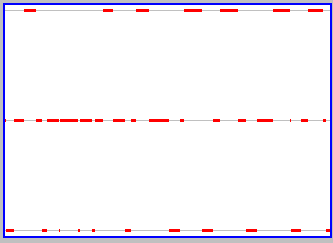 The relation between the properties of the box and the properties of particles begins to change as we add particles (if the particles have the right properties). You can do this yourself, using the active version of the applet (click here if you don't already have it elsewhere on your screen). To get two particles, click to select the lower left window that shows the number of particles on the left side of the box, backspace, type "2", and hit return (your cursor has to be in the window for this to work). Use slow animation and/or "Step" to see the relation between movements of the two particles. Each similarly follows its own path, bouncing off walls when they are encountered, but the initial trajectories of the two are different. This is "having the right properties, and is important, for reasons we'll come back to. Once you've understood what the two particles are doing, click the Graph button to see what is happening to the properties of the box. You should get something similar to what is shown to the snapshot to the right. There are still sharp changes in the properties of the box associated with movement of the particles (broken red lines at the top and bottom of the graph, corresponding to both particles on one or the other side at the same time), but there is an additional state where both sides have the same number of particles (one each) and so the changes in the box are frequently less dramatic (going from both on one side to one on each).
The relation between the properties of the box and the properties of particles begins to change as we add particles (if the particles have the right properties). You can do this yourself, using the active version of the applet (click here if you don't already have it elsewhere on your screen). To get two particles, click to select the lower left window that shows the number of particles on the left side of the box, backspace, type "2", and hit return (your cursor has to be in the window for this to work). Use slow animation and/or "Step" to see the relation between movements of the two particles. Each similarly follows its own path, bouncing off walls when they are encountered, but the initial trajectories of the two are different. This is "having the right properties, and is important, for reasons we'll come back to. Once you've understood what the two particles are doing, click the Graph button to see what is happening to the properties of the box. You should get something similar to what is shown to the snapshot to the right. There are still sharp changes in the properties of the box associated with movement of the particles (broken red lines at the top and bottom of the graph, corresponding to both particles on one or the other side at the same time), but there is an additional state where both sides have the same number of particles (one each) and so the changes in the box are frequently less dramatic (going from both on one side to one on each).
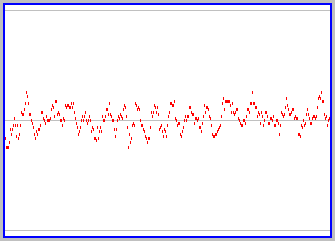 What do you suppose happens as we add more and more particles (obeying the rule that the intial trajectories of each are different)? Try it yourself, using the active version of the applet (click here if its not already somewhere on your screen). The figure to the left shows a snapshot of a graph for a case of 100 particles. There continue to be fluctuations in the proportion of particles on each side, as individual particles follow their own trajectories, but the fluctuations are not as large (we never see all the particles on one side) and the state of the box over time remains close to equal proportions of particles on both sides. You should convice yourself that this gets even more so as one further increases the number of particles involved.
What do you suppose happens as we add more and more particles (obeying the rule that the intial trajectories of each are different)? Try it yourself, using the active version of the applet (click here if its not already somewhere on your screen). The figure to the left shows a snapshot of a graph for a case of 100 particles. There continue to be fluctuations in the proportion of particles on each side, as individual particles follow their own trajectories, but the fluctuations are not as large (we never see all the particles on one side) and the state of the box over time remains close to equal proportions of particles on both sides. You should convice yourself that this gets even more so as one further increases the number of particles involved.
Its important not only to realize that adding things each of which changes can make some other things change less, but to have a feeling for why that happens. If each of the particles followed exactly the same trajectory, it wouldn't happen. Instead, we'd still be in the situation of abrupt changes from all the particles on one side of the box to all the particles on the other. What's important is that the particles follow different and unrelated trajectories ... which means that, at any given time, each has the same probability of being in either the left half or the right half of the box. And so, on average, one finds roughly half on one side and roughly half on the other at any given time. What's staying more or less constant on each side of the box is not any particle, each one is still moving back and forth (watch the green particle while stepping), but rather the collective property of the proportion of particles (whichever ones) on one side of the box and the other. That's Schrodinger's "statistical kind of lawfulness and orderliness". And, far from it "being perpetually disturbed and made inoperative by the unceasing heat motion of the atoms", it very fundamentally depends precisely on that motion.
So ...
- For some things (all?) that appear stable, there is underlying motion and change.
- The motion of water molecules in a quiet lake occurs over time and space scales outside the range which our nervous system are capable of detecting. Within our range, there is only the average ... and hence apparently unchanging behavior.
- For such things, it is as much apparent stability that requires explanation as it is change, since underlying components are always changing.
- It is not only quiet lakes, but also chairs, tables, people, and so forth that don't seem to change (to varying degrees). Why is that? Are they all examples of the same kind of stability or are there different kinds?
- For some things, apparent stability results from statistical averaging of ongoing changes in the parts. For this to happen, its important that the parts be, in some ways, doing different things.
- Lots of things doing the same thing will not reduce and may even enhance some kinds of more global changes. For order, of the kind being considered here, it is critical that different things be changing in different ways.
From stability to change
So, we have an easy way to get at least roughly equal numbers of particles on both sides of the box. Why would we want that? Well, we might or might not, but, in any case, diffusion (the technical name for what we've started exploring) happens all the time, and its a good idea to know why. Put a gas into one side of a box, and it fills both sides equally ... open a bottle of perfume and it can shortly be smelled throughout a room ... put a spoonfull of cream in a cup of coffee and the whole cup eventually gets lighter, even if you don't stir it ... and so forth. We'll see, as we go on, that there are a whole host of physical, biological, and even social phenomena which make sense in terms of diffusion.
Equally importantly, what we've got to this point is a basic driving force, the second law of thermodynamics, which says, at a very fundamental level, why things change: they go naturally and inevitably from statistically less probable to statistically more probable states. As we'll see, it is this movement which life captures and makes use of to move itself it the opposite direction, from less probable to more probable, from disorder to all the organized complexity we think of as life.
| Forum | Back to Playground | Back to Serendip |
Send us your comments at Serendip
 © by Serendip 1994-
- Last Modified: Wednesday, 02-May-2018 10:53:16 CDT
© by Serendip 1994-
- Last Modified: Wednesday, 02-May-2018 10:53:16 CDT
 To appreciate stability and order based on underlying change, one first has to believe there are things changing, and then to see that certain kinds of stability and order emerge as the number of changing things increases ("statistical laws begin to operate", as Schrodinger put it). Let's start with a single moving particle in a large box, the green dot slightly to be left and below the center of the large rectangle (the large box) in the figure to the right, which shows the appearance of an applet we'll use for our explorations. You can get an active version of the applet elsewhere on your screen by clicking here. With it, you'll be able to see that the green dot is actually moving by clicking on the "Go" button. To see the movement more clearly, you can adjust the animation speed using the slider at the bottom of the applet, or click the "Step" button to get one frame at a time. The particle goes about its own business, following a straight line until it hits a wall of the box and then bouncing to follow a straight line until it hits another wall. That's not so surprising or interesting. What's more significant for us is that sometimes there is a particle in one half of the box and no particle in the other, and vice versa, as you can see from the numbers in the small boxes to the lower left and right of the applet. They both intermittently change from one to zero as the particle crosses the center of the box (the tall rectangles to the left and right in the applet also the number of particles on each side in the form of bar graphs, but that's not too impressive with only one particle; it'll be better when we get to working with more).
To appreciate stability and order based on underlying change, one first has to believe there are things changing, and then to see that certain kinds of stability and order emerge as the number of changing things increases ("statistical laws begin to operate", as Schrodinger put it). Let's start with a single moving particle in a large box, the green dot slightly to be left and below the center of the large rectangle (the large box) in the figure to the right, which shows the appearance of an applet we'll use for our explorations. You can get an active version of the applet elsewhere on your screen by clicking here. With it, you'll be able to see that the green dot is actually moving by clicking on the "Go" button. To see the movement more clearly, you can adjust the animation speed using the slider at the bottom of the applet, or click the "Step" button to get one frame at a time. The particle goes about its own business, following a straight line until it hits a wall of the box and then bouncing to follow a straight line until it hits another wall. That's not so surprising or interesting. What's more significant for us is that sometimes there is a particle in one half of the box and no particle in the other, and vice versa, as you can see from the numbers in the small boxes to the lower left and right of the applet. They both intermittently change from one to zero as the particle crosses the center of the box (the tall rectangles to the left and right in the applet also the number of particles on each side in the form of bar graphs, but that's not too impressive with only one particle; it'll be better when we get to working with more).
 Another way to say the same thing is that there is a change in the properties of the box (which side has particles) closely associated with a change in a property of the particle (its location). You can focus more on the changes in the state of the box by clicking on the "Graph" button on the active applet. This gives a display of the state of the box as a function of time, a snapshot of which is shown to the left. The middle grey line corresponds to both sides of the box being equally occupied by particles. More particles on one side is upwards from this line, and more particles on the other side downwards. With only one particle, the box repeatedly shifts from a state of all particles on one side (the upper broken red line) to a state of all particles on the other (the lower broken red line). There is, as we said above, a very close relation between a property of the particle and a property of the box.
Another way to say the same thing is that there is a change in the properties of the box (which side has particles) closely associated with a change in a property of the particle (its location). You can focus more on the changes in the state of the box by clicking on the "Graph" button on the active applet. This gives a display of the state of the box as a function of time, a snapshot of which is shown to the left. The middle grey line corresponds to both sides of the box being equally occupied by particles. More particles on one side is upwards from this line, and more particles on the other side downwards. With only one particle, the box repeatedly shifts from a state of all particles on one side (the upper broken red line) to a state of all particles on the other (the lower broken red line). There is, as we said above, a very close relation between a property of the particle and a property of the box.
 The relation between the properties of the box and the properties of particles begins to change as we add particles (if the particles have the right properties). You can do this yourself, using the active version of the applet (click
The relation between the properties of the box and the properties of particles begins to change as we add particles (if the particles have the right properties). You can do this yourself, using the active version of the applet (click  What do you suppose happens as we add more and more particles (obeying the rule that the intial trajectories of each are different)? Try it yourself, using the active version of the applet (click
What do you suppose happens as we add more and more particles (obeying the rule that the intial trajectories of each are different)? Try it yourself, using the active version of the applet (click