Information?: An Inquiry Tuesdays, 9:30-11 am Science Building, Room 227 Schedule | On-line Forum | Evolving Resource List For further information contact Paul Grobstein.

Al (see his notes) rose to the challenge of making clearer the perspectives of physics (and physicists) on reversibility/irreversibility, time, and the meaning of information in relation to perspectives of biologists/neurbiologists/linguists that were discussed last week.

Al began by asserting that physics/physicists were not in fact committed to time irreversibility. The Boltzmann explanation of the second law in fact included an element of irreversibility inherent in the "coarse-graining" used to characterize microstates. Boltzmann was severly criticized by other physicists both for this feature of his explanation and for a dependence on observer resolution inherent in the definition of macrostates (as well as the failure to explain the origin of macroscopic reversibility from local reversible processes). The advent of quantum physics provided an explanation of coarse-graining in terms of the uncertainty principle (though there are issues of whether the scales of the two processes correspond quantitatively) but exacerbated the observer dependence problem by implying that coarse graining was itself an observer-dependent phenomenon, ie that irreversibility was associated wave function collapse associated with "observation" or "measurement".

Considerable discussion led to the following figure and ideas:

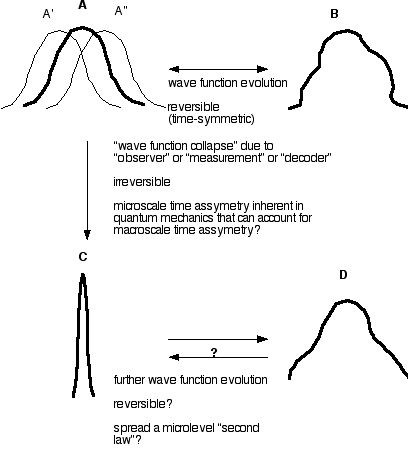
Quantum physics uses time symmetric equations to describe (with extraordinary precision and success) the evolution of wave functions which represent the probability (squared) of entities exhibiting particular properties. A and B in the figure above are imagined wave functions showing probabilities (plotted vertically) of, for example, the location of a particle (one dimension plotted horizontally). The transition from A to B is time-symmetric, ie it is both deterministic and reversible.

The wave function itself is neither observable nor measurable. When a measurement is made (as for example of the position of a particle), the wave function is said to "collapse", ie a description of the probabilities of the particle being at a large number of locations is reduced to a description of the location of the particle (to some degree of precision). This transition (from A to C) is in an important sense an "irreversible process". The "irreversibility" results from the fundamental "indeterminacy" of this transition, ie the observed state is not one to one with the wave function but is one of a number of possible states for which the wave-function describes the relative probabilities. A consequence of this indeterminacy is that many different wave-functions (A' and A" among them) could each collapse to the same observed state, and hence there is no way to go "backwards" to specify the particular wave-function from which the observed state derived.

This might be thought of as a relatively insignificant point if the future evolution of the wave function were not affected, ie if irrespective of the transition A to C, the transition A to B (and all future deterministic evolution of wave function) continued to occur. In this case, the collapse (and any subsequent collapses) would be epiphenomena, meaningful to humans but not important to the quantum description of "reality". It appears through that the collapse does in fact influence the subsequent wave function, which is derived from the collapsed state in the transition C to D and so is different from B. This makes the collapse meaningful not only for "observations" but also for the evolution of the quantum description itself. And raises some interesting questions about the C to D process. It would seem to necessarily involve an increase in wave function spread. Is this a "spontaneous" process? an information addition process? a micro-analog to the macro second law? a reversible or an irreversible process? In any case, it is relevant that on this intepretation there is some but not complete indeterminacy in going from A to C. C is not fully predictable from A but is correlated with A in the sense that only some C's can evolve from A (the set may be infinite but is certainly bounded).

It did not escape the notice of some discussants that there are close parallels between at least some of the ways quantum behavior was considered and some of the ways we were talking about language and the nervous system last week. In particular, the collapse of the wave function can be thought of as involving a "loss of information", ie as with a filtering network there is a convergence of lots of different possibilities into the same conseqeuence. Perhaps the parallel is even closer in the sense that there is also an information "gain" (both loss and gain being defined in the traditional Shannon sense) as there is in filtering networks, ie the resultant is an interaction between the wave function and the "observer" or "measurer" who contributes some information (a categorization scheme?) to the resultant. If so, it may be possible to think of the collapse of the wave function in the same terms as "categorization", a process of simultaneous Shannon information loss/gain which in turn lays the foundation for information creation.

There remain issues to be clarified about the this line of interpretation of quantum phenomena and its relation to other aspects of physics. Among ones noted are the role and significance of "phase" and possible problems related to conservation of energy. Should the parallels between last week's discussion and this week's prove to be robust, it would suggest that in important ways the problems of coming up with a more useful definition of "information" may be common to both physics and linguistics/biology and that experiences/perspectives in the latter arena may be relevant in the former. In both cases, there are issues of "observer", "process", and "meaning" that seem not well characterizable in terms of traditional Shannon concepts of information, and might perhaps be better dealt with in terms of an earlier idea that "information" is a non-random pattern that is transformed by a non-random process into another non-random pattern. This focuses attention more on "information processing" than on information per se and includes some elements of both context and "meaning" that are missing from the Shannon formalisms. It also remains, at worst, agnostic about the virtues or lack thereof of time asymmetry and irreversibility and, perhaps at best, opens the possibility that these are not only permissable but desirable.

There are two particular places where there may be, in addition to potentially interesting parallels, some more concrete intersections between issues in physics and those in linguistics/biology/neurobiology. Zelinger, in trying to answer Wheeler's question "why the quantum?" makes use of the idea that all of physics consists of answering yes/no questions and that without a base "simplest" proposition (the "bit") one is condemned to an infinite regress of questions and an "infinity" of information. While this might provide a useful story for (some?) physicists, it raises for (at least some) others the unanswered questions of who is asking the questions and why whoever-it-is has a distaste for infinite regresses and infinities of information. Is it nothing more than "reinventing rationalism"?

A possible answer to these concerns is that physics is a product of the human brain (with the presumption that it is humans who are asking the questions and have a distaste for ...), and Al pointed to at least some physicists who offer this position explicitly. The invitation to account for both quantum phenomena and "information" simply in terms of brain idiosyncracies was, however, declined by at least one neurobiologist (to the shock and distress of one logician) citing arguments by another physicist. The argument, basically, is that the history of physics (and other sciences) is largely one of noticing that aspects of scientific stories might depend on idiosyncracies of the observer, controlling for those idosyncracies, and discovering that there remain significant regularities apparently not accounted for by the brain (see Peter Kosso, Appearance and Reality: An Introduction to the Philosophy of Physics). While it is in principle conceivable that this process would ultimately exhaust observable "external" regularities, it seems a better bet to presume that there is indeed "something" out there and that that something, as well as brain characteristics, are what is reflected to varying degrees in all scientific stories. To put it differently, one can acknowledge not only "subjectivity" and even its inevitability without giving up the presumption of something out there independent of the brain and the ambition of "getting less wrong" in the brain's description of it.

An argument was made that both the wave-function collapse and "information" must have elements of this "out there" character to them, and that the linkage between the two might be quite direct. Physicists have long puzzled about what causes the collapse of the wave-function, entertaining at various times the possibilities that it was due to human observation, measurement, and/or consciousness without yet achieving a consensus on that matter. In fact, any notion of an essential involvement of humans in the collapse of the wave-function seems unlikely since humans have been in existence for only a quite recent and very short part of cosmic evolution, and cosmic evolution is (at least currently) accounted for largely in terms of classical rather than quantum processes. This suggests that the wave-function was collapsing long before humans came into existence (indeed long before brains or even living organisms (model builders?) came into existence).

Are there things that are "meaningful" "out there"? That are causally significant among themselves whether humans/consciousness/brains are around or not? Movements of the air as opposed to "sound"? Both "mass" and "energy" seem to have that "out there" character. at least it has not yet been suggested that consciousness or humans played a causal role in the orbiting of planets around the sun. Might there be a way to think of "information" similarly? Could it for example be that what causes the collapse of the wave function isn't an "observer" or a "measurer" but rather interaction with a "decoder", ie any "non-random distribution of matter/energy that non-randomly transforms one non-random distribution into another"? This might explain why wave-function collapse seems to have been a ubiquitous feature of "reality" for a very long time as well as why physicists have to work so hard to maintain things in an indeterminate state (wave function collapse becomes likely as soon as there are non-random distributions of mass/energy around; there are currently lots around).

Following this line of thinking would require one to regard "random" vs "non-random" as a "fundamental" distinction (ie one not dependent on the presence of human brains). There was disagreement about why one would want to do this as well, whether it could in fact be done, and, if so, how? Is the "random" / "non-random" distinction robust in the sense of human-independent? As a statistical idea (either classically or in Bayesian terms?)? Could "randomness" be equated with "absence of causal relationships" or with particular kinds of causal relationships? Is there an important relation between randomness and irreversibility and could these be used to derive a rigorous/quantitative theory of information beginning with the decoder notion? Perhaps in combination with the idea that some (all?) decoders simultaneously both eliminate and create information in the original Shannon sense of the term?

Home | Calendar | About | Getting Involved | Groups | Initiatives | Bryn Mawr Home | Serendip Home

Director: Liz McCormack - emccorma@brynmawr.edu | Faculty Steering Committee | Secretary: Lisa Kolonay
© 1994- , by Center for Science in Society, Bryn Mawr College and Serendip
Last Modified: Wednesday, 02-May-2018 10:51:19 CDT