 Under construction!!!
Under construction!!!
Period-3 Points
In the Dynamical System Theory of the sixties and seventies there were two distinct approches. On one hand the topologysts explained geometrical properties to establish results about systems they hoped had some connection with nature. In the seccond approach phisycists started from equations which they knew had connections with the real world, found solutions with the help of computers and discovered similar structures to those that topologists where formulating. Nevertheless, the scientists were aware that those computer calculations where just approximations of the description of a dynamical system.
For example, the logistic map is a mathematical description of a dynamical system. In the formula
k is a parameter which takes values between 0 and 4.
The way one computes the iterations is using the following formula:
If we experiment with k between 0 and 3 we observe that we always obtain attracting fixed points.
For k=3 the fixed point is 'marginally stable', in other words convergence to it is very slow.
For k between 3 and 4 we have orbits of all periods.
Li and Yorke proved that if the logistic map has a period-3 orbit then it has all other periods. Next we will show a proof of their claim.
Li-Yorke Theorem
It can be seen from the graph below that the logistic map is continuous. All we have to show is that f([0,1]) is contained in [0,1]. f(x) is always greater or equal to 0 since k=3.84 and, for x in [0,1], x and 1-x are always positive numbers. The maximum value of the logistic map is obtained for f'(x)=0, wich means x=1/2. But f(1/2)=0.96, thus f([0,1])=[0,0.96], which is contained in [0,1].
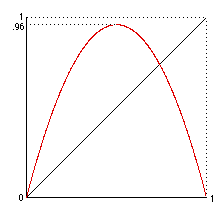
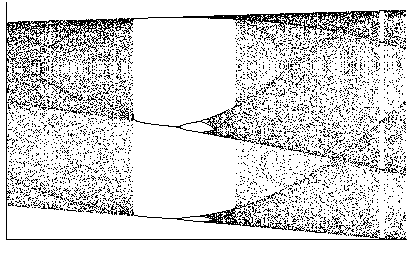
From the biffurcation diagram (picture below) we can observe that the logistic map has a period-3 orbit (for k=3.84).
In order to prove Li-Yorke Theorem we need to prove some preliminary theorems and a few lemas.
Maximum-Minimum Theorem
Suppose that f is continuous on the interval [a,b]. Then f has a maximum and a minimum value.
Proof:
From Lemma I we know that the range of a function continuous on a finite closed interval is itself a finite closed interval. Thus the extreme values of f are the endpoints of the interval f([a,b]).
Intermediate Value Theorem
Suppose that f is continuous on the interval [a,b] and let p be any number between f(a) and f(b). Than there is a number c in [a,b] such that f(c)=p.
In other words, f can not skip over any values between f(a) and f(b).
Proof:
Proof by contradiction.
Suppose we have a point p between f(a) and f(b) such that for any c in [a,b], f(c) is not p. Since c is between f(a) and f(b) which are in [m,M] (where m and M are the extreme values from preceding theorem), then c is in [m,M]. Thus f([a,b])=[m,p)+(p,M]. But [m,M] should be a closed interval. Thus there is no p in [m,M] that satisfies our assumption. Hence, for any p in [f(a),f(b)] we can find c in [a,b] such that f(c)=p.
Lema I.
Let f be continuous on an interval J. Let f(J) denote the colleclion of all values f(x) for x in J. Then f(J) is also an interval.
Proof:
We will prove this lema by contradiction.
Suppose thal f(J) were not an interval. Then there would exist two numbers y and z in f(J), with y<z, and a number p in (y,z) such that p is not in the range of f. By the Intermediate Value Theorem applied to [y,z], the range of f must contain the entire interval [y,z], and in particular must contain p. This contradiction implies that f(J) is an interval.
Lema II.
Let f be continuous on a closed interval J, and assume that f(J) includes [a,bl. Then there is a closed interval K such that J includes K and f(K) = [a,b].
Proof:
Since f(J) contains [a,b], there are numbers x and z in J such thal f(x) = a and f(z) = b. Among all such numbers z, there is one that is the closest to x. Call it y (Figure 1, where J = [r,s]). Since f is continuous implies that y exists. Similarly, there is a w between x and y that is the closest to y for which f(w)=a. By Lemma I, the closed interval K detemmined by w and y (which is either [w,y] or [y,w]) has the property thal f(K)=[a,b].
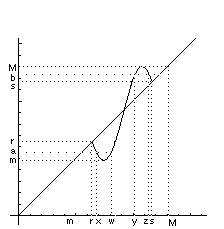
Figure 1.
Lema III.
Suppose that J is a closed interval, and assume that f is continuous on J and f(J) contains J. Then f has a fixed point in J.
Proof:
By the Maximum-Minimum Theorem, f has a minimum value r and a maximum value s on J, so for suitable y and z in J,
s=f(z) is a maximum value of f on J
Since r is the minimum value of f(J) and s is the maximum value of f(J), and since f(J) includes J. it follows that r<y<s and r<z<s. Now let g(x)=f(x)-x. Then g is continuous on J since f is. Furthermore,
and
g(z)=f(z)-z=s-z>0.
Lema IV.
Let f be continuous and suppose that f(a)=b, f(b)=c and f(c)=a. Then f has a fixed point and a period-2 point.
Proof:
Without loss of generality we may suppose that a<b<c (otherwise change them inbetween). Since f(b)=c and f(c)=a (Figure 2.(a)), we know that f([b,c]) which includes [a,c] includes [b,c], so by Lemma III, f has a fixed point in [b,c].
(a)
Figure 2.
(b)
To show that f has a period-2 point, let m be the largest number such that a<=m<b and f(m)=b.
Since f is continuous on [a,b] and since f(b)=c>b, such an m exists.(by the Intermediate Value Theorem since b is contained in [f(a)=b,f(b)=c) and thus exists m in [a,b) such that f(m)=b.
Then f([m,b]) includes [b,c], so that
f[2]([m,b]i>) includes f([b,c]) includes [a,c] which includes [m,b].
By Lemma III, with J=[m,b], there is a fixed point p of f[2] in [m,bl (Figure 2.(b)). Since m<b<c, f(m)=b and f(b)=c, we know that p<>m and p<>b. It follows from the definition of m that if m<x<b, then f(x)>b, so that f(p)>b>p. Therefore p is not a fixed point of f, so p is a period-2 point of f.
(You can check in Figure 2.(b) that p is indeed a period-2 point of f.)
Proof of Li-Yorke Theorem:
Let's first assume that a<b<c and let f(a)=b, f(b)=c and f(c)=a. (if a,b and c has other order, just change them inbetween; if f(a)=c then f(c)=b and f(b)=a, and the proof follows simmilarly). By Lemma VI. f has points of period 1 and 2. Also we assume that f has points of period 3. Now let n>3. We claim that f has points of period n. We have to show that there is a point p in [b,c], such that:
i. f[k](p) is in [b,c] for k=1,2,...,n-2
ii. f[n-1](p) is in (a,b)
iii. f[n](p)=p is in [b,c].
Then p will have period n. To prove that f has a period-n point will procede as follows. Let J0=[b,c]. We know that f(J0)=f([b,c]) includes [a,c], which includes [b,c]=J0.
The second lemma assumes the existence of a closed interval J1 included in J0 and
Next f[2](J1)=f(J0) that includes J0 and by Lemma II. there is a closed interval J2 such that J1 includes J2 and f[2](J2)=J0. So
f[3](J2)=f(f[2](J2))=f(J0)
that includes J0, and again by Lemma II. there exists an closed interval J3 included in J2 and f[3](J3)=J0. By induction we obtain a nested sequence of closed intervals J0,J1,...,Jn-2.
and we can write
Jn-2 include in Jn-3 included in ..... included in J1 included in J0=[b,c]
and
f[k](Jk)=J0=[b,c], for k=1,2,...,n-2.
Therefore
so by Lemma II. there is a closed interval Jn-1 included in Jn-2 and
It follows that,
f[n](Jn-1)=f(f[n-1](Jn-1))=f([a,b]) includes [b,c] includes Jn-2 includes Jn-1.
From Lemma III. we know that there is a point p in Jn-1, and hence in [b,c], that is a fixed point of f[n]. To show that p has period n we first observe that f[k](p) is in [b,c] for k=1,2,...,n-2 because for each k, p is in Jk and f[k](Jk)=[b,c].
Next we will complete the proof that p has period n by showing that f[n-1](p) is in [a,b). Recall that f[n-1](Jn-1)=[a,b]. Since p is in Jn-1 we know that f[n-1](p) is in [a,b]. If it were true that f[n-1](p)=b, then
p=f[n](p)=f(f[n-1](p)=f(b)=c
so that f(p)=f(c)=a. However, since Jn-1 included in Jn-2 included in J1 and p is in Jn-1, it follows that f(p) is in f(J1)=[b,c], so that f(p) is not equal with a. This contradiction implies that f[n-1](p) is not equal to b so that f[n-1](p) is in [a,b). Hence all n-2 iterates of p are in [b,c], the n-1 iterate is in [a,b) and the nth iterate is again in [b,c]. Thus p has a period that divides n. Since we have just one element in [a,b] and all the others in [b,c] and since the orbit is containing always the same points, then there is just one orbit of period n, thus p has period n. This completes the proof in the case f(a)=b, f(b)=c, f(c)=a. For f(a)=c, f(b)=a, f(c)=b, the proof is similar.
Figure 4. - The Biffurcation Diagram for the Logistic Map

Send any comments to: bbutoi@brynmawr.edu
[an error occurred while processing this directive] © Bogdan Butoi '96 - Last Modified: Wednesday, 02-May-2018 10:51:09 CDT - Number of visitors: [an error occurred while processing this directive]